This tutorial will walk through calculating three key summary measures of variability in data - range, IQR, and percentile.
Python Code Screenshot
Range, IQR (Interquartile Range), and Percentiles are all summary measures of variability in the data. As we learned in the last post, variance and standard deviation are also measures of variability, but they measure the average variability and not variability of the whole dataset or a certain point of the data. This is where other statistical measurements help us break up the data into parts for easier understanding of variability. Additionally, these metrics are easier to solve for so range, IQR, and percentiles are all used as shorthand calculations to check for how dispersed your data might be.
Range
Range is the simplest of the measurements but is very limited in its use, we calculate the range by taking the largest value of the dataset and subtract the smallest value from it, in other words, it is the difference of the maximum and minimum values of a dataset. Take this set of numbers: 1,3,3,3,4,5,4,5,10, the range is (10-1) which is 9. However, if I change the 10 to 1000 in the dataset the range is 999. Therefore, the range is very susceptible to outliers and does not measure how clustered the data is. We will not be using it much, but it is important to learn about it and its drawbacks as they are motivations for the other measurements we will discuss in this post.
Percentile
Percentile is an interesting measurement that you have probably heard in the context of test scores or your height and weight. Therefore, this is the first relative measurement of dispersion, meaning that it is scored in reference to the other data in the dataset. Before diving into solving percentiles – let’s examine what this statement means; “Ben scored in the 75th percentile on the SATs”. Does this mean that Ben scored a 75 or that he has the 75th best score? No, not at all, this does not tell us anything about Ben’s score or how many data points they are. Rather, this statement means that Ben scored better than 75% of the other test-takers, which means Ben scored worse than 25% of the other test-takers. If you read the previous posts we spoke about median, now take a second and think about how the median can relate to percentiles? The answer is median, the middle value is another name for the 50th percentile.
If the median is a type of percentile, what was the first step to solving for the median, ordering the dataset from smallest to largest? The next step is to multiply the total number of values in the dataset by the percentile you want. The result of this step will give you the index, keep in mind if the index is not a whole number round it to the next whole number. Now that we have an integer as our index, count the values in your dataset from left to right until you reach the index value. This is a very similar concept to the median and we saw that Python zero indexes which can lead to some careless errors, so be careful!
IQR
The last topic we will discuss is the interquartile range which is a measurement of the difference between the third quartile and the first quartile. The first quartile, known as Q1, is the value of the 25th percentile and the third quartile, Q3, is the 75th percentile. The IQR is a better and more widely used measurement because it measures the dispersion of the middle pack of data and is less sensitive to outliers.
Step-by-Step Tutorial
Now that we understand these measurements, let’s go over how to calculate them in Python using no packages as the formulas to solve for these three measurements are remedial.
-
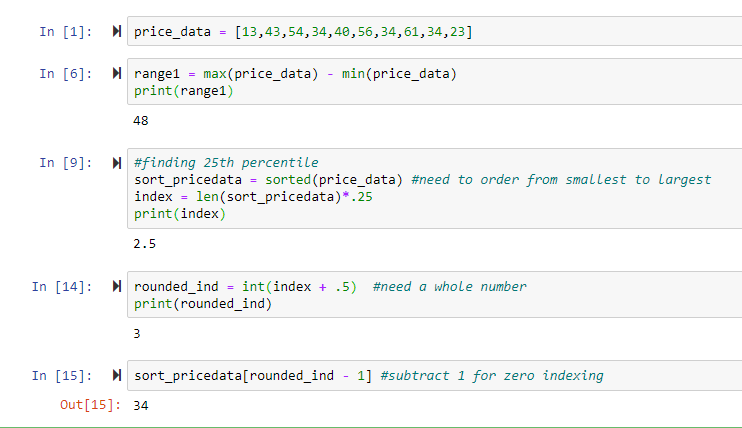
Step 1: Create a list called price_data and populate it with the values above
-
Step 2: Create a variable called range1 and set it equal to the difference between the max and min of the dataset and print the range.
-
Step 3: Create a variable called sort_pricedata and set it equal to sorted(price_data), this sorts the data from smallest to largest which is a necessary first step in finding the percentile.
-
Step 4: Create a variable called index and set it equal to the length of the data and multiply it by the percentile that you want to look for, in this case, the 25th percentile (.25). Print the index to see if it’s a whole number.
-
Step 5: Create a variable called rounded_int and set it equal to your index added to .5 so it rounds up to a whole integer.
-
Step 6: Index the sort_pricedata by the rounded index minus 1 (to adjust it for zero index) to get the number that is the 25th percentile of the data.
*Bonus Exercise: Repeat Steps 3-6 with the 75th percentile and then take the difference of the 75th percentile and 25th percentile to get the interquartile range.
